How GPR works?

Understanding wave propagation is important to how Ground Penetrating Radar (GPR) works. GPR uses electromagnetic (EM) waves to probe the subsurface. A transmitter sends EM pulses through a medium. These waves travel through different materials, reflect off objects or boundaries and return to the surface, where they are recorded by a receiver. The way these waves propagate -how they travel and interact with materials- determines the signals we receive. The propagation of GPR waves is strongly influenced by the dielectric properties of the materials they travel through, unlike to conventional radars, where the waves travel through air. When there is a contrast in these properties, part of the EM energy is scattered and/or reflected, while the rest of the energy continues travelling through the medium. The magnitude of the reflected signals depends on the contrast between two materials. Higher contrasts (e.g. between dry concrete and metal or dry soil and wet soil) produce strong reflections, whereas low contrasts result in weaker reflections.

An example of wave propagation is shown below. On the left plot, the waves emitted from the receiver and propagated in the subsurface are shown. On the right, when the propagating waves encounter a dielectric contrast between the target and the surrounding medium, they are reflected and travel back to the receiver.

Note that for GPR, it is important for dielectric contrasts to exist between different materials in order to be detectable. The interface of two different materials with the same or very similar dielectric properties, will not yield a reflection, and thus a target might be undetected. One example is glass-fibre bars used as reinforcement inside concrete slabs. The properties of the bars are often very similar to the surrounding concrete’s and thus, the bars will remain undetected by GPR. This is not a limitation of a specific system, but of the physics behind EM propagation.

Dielectric properties

The dielectric properties describe the behaviour of materials under the influence of electric and magnetic fields.  The properties determine how fast the waves travel, how much they reflect and how quickly they attenuate (lose energy). These properties are the dielectric constant (relative permittivity), electric conductivity and the magnetic permeability:

Dielectric constant (Relative permittivity): The dielectric constant measures how much a material slows down the EM waves compared to their speed in vacuum. In vacuum, the waves travel with the speed of light c and the dielectric constant of vacuum is ε=1. Materials with higher dielectric constants (e.g. water, wet soil) slow the wave down more, while materials with lower dielectric constants (e.g. dry sand) allow faster propagation. The velocity of wave propagation through a material, which allows us to find depth to targets, is inversely proportional to the square root of the dielectric constant:

To understand the effect of the dielectric constant, an example is given below. A metallic reinforcing bar is placed at the same depth inside of two different materials. The data on the left correspond to a low permittivity medium (e.g. dry sand) and on the right to a high permittivity medium (e.g. wet concrete, wet clay). It is obvious, that the hyperbolic response from the bar is received much later in time when in the high permittivity medium due to slower propagation compared to the low permittivity medium.

Conductivity σ determines how much a material absorbs and dissipates EM energy as heat. High-conductivity materials, such as clay or saltwater, cause rapid attenuation of the signals, resulting in weaker received reflections and reduction in penetration depth. The attenuation accounts only for one part of the total energy losses, with other important ones being the geometrical spreading losses of the waves propagating outwards in a material and scattering losses from small inhomogeneities in the subsurface. To show the effect of conductivity, an example is given below from a buried metallic reinforcing bar. The B-scan on the left corresponds to a material with zero conductivity, whereas the B-scan on the right corresponds to a material with a finite conductivity. It is obvious that the response from the rebar on the right plot is much weaker due to the attenuation compared to the one from the left with zero conductivity.

Magnetic permeability: Refers to how a material responds to the waves’ magnetic fields.

Although the materials that are encountered with GPR are complex (natural or man-made), most of them are non-magnetic, having a permeability close to free space. For GPR, the dielectric constant and conductivity hold the most important role. The dielectric constant of materials commonly investigated by GPR can vary significantly, especially in the presence of water in the medium. Most common materials have a permittivity value that falls in the range of 1-81. The presence of water significantly increases the bulk dielectric constant of a material, because the water has a high dielectric (~81).

Frequency, resolution and penetration depth

In GPR, the frequency of the EM wave directly impacts the resolution of the data (how small features we can resolve) and the penetration depth (how deep the signal can travel into the subsurface). There is a trade-off between resolution and penetration depth. High-frequency antennas offer better resolution and can detect small targets but can penetrate only at shallow depths. These antennas are used in applications such as detecting rebars in reinforced concrete or mapping shallow archaeological features. Low-frequency antennas penetrate deeper but provide lower resolution and thus cannot detect small features. These are suitable for detecting large and deeper targets as in utility detection, road inspections and geological surveys.

GPR systems are ultra-wideband systems and thus, transmit a whole range of frequencies and not only a single frequency. However, each frequency is transmitted with a different energy, which depends on the characteristics of the antenna itself.

The environmental conditions have also an effect on resolution and depth. Wet or clay-rich soils absorb GPR signals more quickly, reducing penetration depth. In some cases, even low-frequency antennas might not be able to achieve significant penetration in these soils. Dry soils allow for much deeper penetration, even for higher frequencies. For heterogeneities existing in the subsurface, higher frequencies provide more detailed data but may be prone to more signal clutter.

Data Representation

Data obtained from a GPR system is typically displayed in a variety of visual formats that help interpret the subsurface features. The most common representations are A-scans, B-scans and C-scans and less common but very useful is the 3D volumetric representations.

A-scan/Trace/Wiggle

An A-scan or Trace or Wiggle is the simplest form of GPR data representation. It is a 1D plot of GPR signal amplitude (strength of the reflection as voltage) versus time and provides information locally, at the vicinity of the measurement point. It records the reflected signals vs two-way travel time, where two-way travel time is the time it takes from waves to travel from the transmitter to a subsurface target and then back to the receiver after reflecting off the target. It is essentially a round trip from the surface down to an object/layer and back again. The time is often converted to depth using an estimate of the EM wave velocity in the subsurface, and thus the A-scan will show the signal amplitudes plotted vs. depth.

An A-scan is collected at a single measurement location, as shown below, where the GPR system (transmitter and receiver in the same enclosure) is placed directly above a target.

An example of an A-scan (amplitude vs. time) is shown below.

The first reflection on an A-scan usually corresponds to the surface reflection (including the direct air wave), whereas subsequent reflections coming later on time, represent interfaces or objects, such as soil layers, voids or pipes.

B-scan/Radargram

Collecting A-scans at different measurement points along a line produces a B-scan or Radargram, which is presented as a 2D image in time and space that shows how the GPR signals reflect from different subsurface features along this line. The B-scan (radargram) is the most widely used representation of GPR data.

A B-scan is generated by moving the GPR antenna along a survey path (scanning direction), with the GPR system continuously emitting pulses and recording the reflected signals at each point. An illustration of B-scan collection is shown below, where the GPR system is moved along a line at regular intervals above a target.

Similarly to the A-scans, a B-scan displays the recorded signals in the form of amplitudes vs. two-way travel time. The y-axis in a B-scan represents the two-way travel time or depth, the x-axis represents the distance along the survey line and the plotted amplitude values show the intensity of the reflections. Each pixel of the B-scan image has a color associated with the magnitude of the received signal. An example of a B-scan is shown below, along with the plotted A-scans (red color).

From a B-scan, it is much easier to detect features than from individual A-scans, as in a B-scan, we can see the hyperbolic reflection patterns created when scanning perpendicular to the long axis of objects such as pipes or rebars, but also it is easier to see layers in the subsurface, such as pavement layers, which appear as a flat long response in B-scans.

C-scan or slice

C-scan or time/depth slice is a 2D horizontal image that represents reflections from a specific time/depth in the subsurface. They are essentially slices of the subsurface taken at varying depths, providing a plan view of subsurface features. Slices are generated from a grid of GPR survey lines collected over an area. The data from the multiple survey lines are combined to create a 3D representation. From this dataset, horizontal slices at different depths or time intervals are extracted. Each slice covers a particular depth/time range, referred to as slice thickness. The x-axis and y-axis in a slice represent the horizontal position within a survey area whereas the plotted values represent the signal amplitudes.

An example of two slices taken from the same GPR dataset at different depths is shown below.

3D volumetric representations

The whole dataset, that includes data collected from multiple lines, can be used to generate a 3D volume and analyze features in all three dimensions instead of individual cross-sections or slices. However, this is very computationally demanding.

Why data processing is needed?

Processing GPR data is essential for various reasons to ensure accurate and interpretable results. Raw GPR data often contains noise and clutter and the signals are weak making it difficult to identify and interpret subsurface features directly. The purpose of data processing is to improve the quality of the data and enhance the visibility of important subsurface features. Some of the reasons why GPR data needs to be processed are:

1)    Noise Clutter reduction: GPR systems often pick up noise from various sources such as EM interference, reflections from surface objects but also unwanted reflections from subsurface objects and environmental factors, known as clutter. Processing helps remove or minimize this noise, making meaningful reflections more apparent and easier to analyze.

2)    Signal enhancement: Some subsurface features, such as deeper objects, may produce weak radar signals that can be difficult to detect in the raw data. Processing, such as gain, can be used to enhance weaker signals so that they are more visible in the B-scans.

3)    Position correction: Subsurface objects can appear to be in the wrong position in GRP data. Processing can help re-position the reflections at their correct locations, providing a clearer image of the subsurface.

Common GPR data filters

Time zero correction

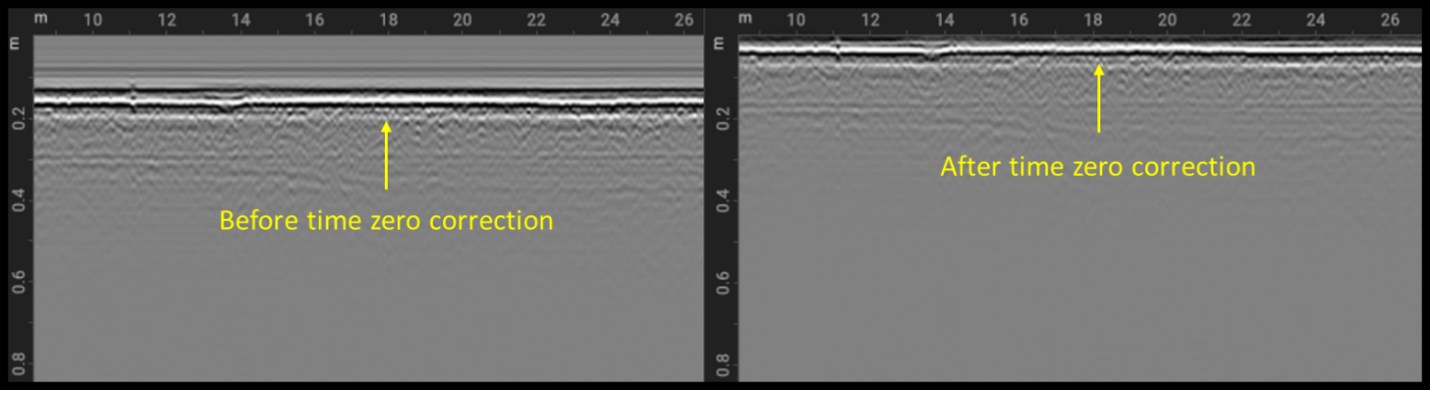
Time zero is the time when the transmitter starts off the signal transmission. To make an accurate interpretation of the depth of subsurface objects from the GPR data, knowledge of the time zero is needed. However, due to time delays associated with the instrumentation itself, it is not possible to determine the exact time that the transmitter emits. Thus, to compensate for this, a time-zero correction should be applied in order to shift the responses so that the time-zero corresponds to the surface reflection.

Time zero correction is different for different GPR datasets and finding the optimal time zero value for accurate depth estimations is one of the problems faced during processing. This depends on both the GPR instrumentation used but also on the antenna separation. Different points have been suggested for time zero correction with the most common ones being: the first break, which is the time point when the receiver starts recording the direct wave transmitted by the transmitter, the time corresponding to the positive or negative peak amplitude of the responses, or the time corresponding to the first zero amplitude point between the first positive and negative peak. Time zero correction is usually the first processing step applied on GPR data.

An example of the effect of time zero correction can be seen below, where on the left we can see the direct wave response located at ~0.16 m and on the right, the same response located at 0 m after time zero correction.

Background removal

Background removal is one of the main GPR data processing steps. This method is used to suppress coherent system noise appearing as bands or/and remove other horizontal events in GPR data. The bands are horizontal events that exist in the data and are present across the entire length of a B-scan. In addition, it is used to remove the direct air wave from transmitter to receiver and the direct ground wave corresponding to the interface between air and subsurface.

Frequently in GPR images, the target signatures are masked by the direct air and direct ground wave responses, together called direct wave, due to having a stronger signal. Therefore, apart from suppressing system noise, the background response can be removed from the total responses in order to enhance other events. Note that in addition to the background, other flat-lying responses that might be of interest will be removed/partially removed during this filtering process, therefore always check the raw data as well before applying this filter.

Background removal is most commonly performed by subtracting the mean A-scan of all the A-scans in a GPR line (B-scan) from every A-scan in that line. By default, to perform this, all traces in a B-scan and the whole time window (total time an A-scan was recorded) are selected. Different variations of this method exist that can be used based on the needs of a GPR dataset, such as using only a certain number of traces or using a time window smaller than the total recorded time.

An example of a B-scan collected over a concrete slab with a rebar grid is shown below. On the left plot, we can see the data before background removal. Here, the direct wave is visible on the top of the B-scan and also horizontal events that correspond to rebars, which were collected while scanning parallel to the long axis of the rebars. There are also some ‘hidden’ responses in the B-scan, which are masked. On the right plot, we can see the resultant B-scan after applying background removal. The masked responses from the rebars (hyperbolas) are now visible. These were obtained by scanning perpendicular to the long axis of these rebars and thus produce the characteristic hyperbolic pattern. Note also that the direct wave and other flat lying events have now been removed and therefore care must be taken not to miss important features during interpretation.

Gain adjustment

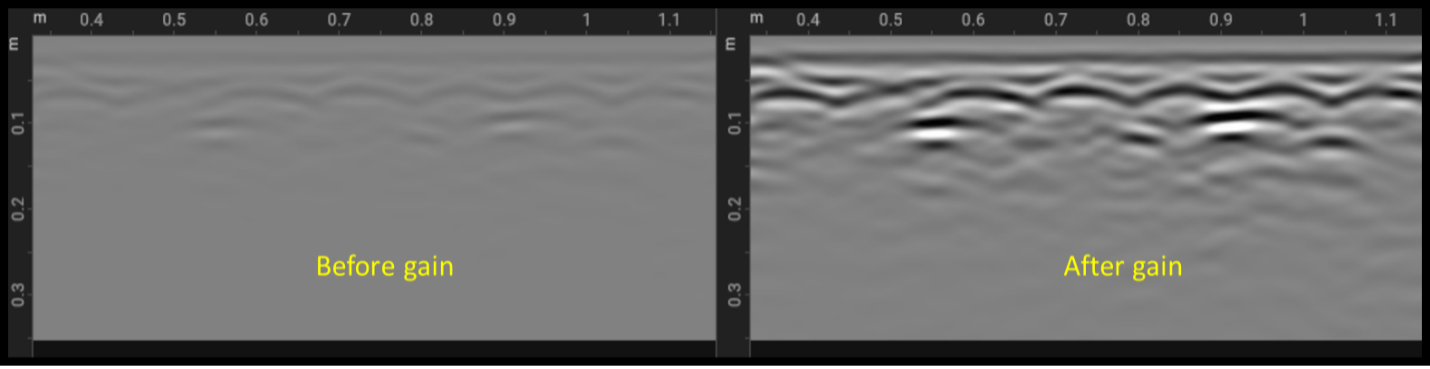
As the EM waves get attenuated while they are travelling through the subsurface, the returned signal from a target is weaker in amplitude compared to the one from the surface. To compensate for that, gain can be applied to amplify the responses arriving later in time (deep subsurface objects) and other weak responses (corresponding to small dielectric contrasts) in order to make them clearly visible. This is usually a non-linear operation implemented with a function that increases the amplification with time in order to compensate for the weaker signals. Gain changes the frequency content of the signals and thus, the amplitudes and shapes of the original responses.

There are different gain techniques, some of which:

Constant gain: Applies the same amplification across the entire B-scan

Linear gain: Increases gain linearly with depth

Exponential gain: Applies an exponentially increasing gain with depth

Automatic Gain Control: A type of gain control that dynamically adjusts the signal amplitudes based on the strength of the incoming signal by calculating a gain curve.

An example of gain is shown below. On the left plot, we can see the B-scan before gain where the responses are faint, whereas on the right, we can clearly see the hyperbolas and flat event response.

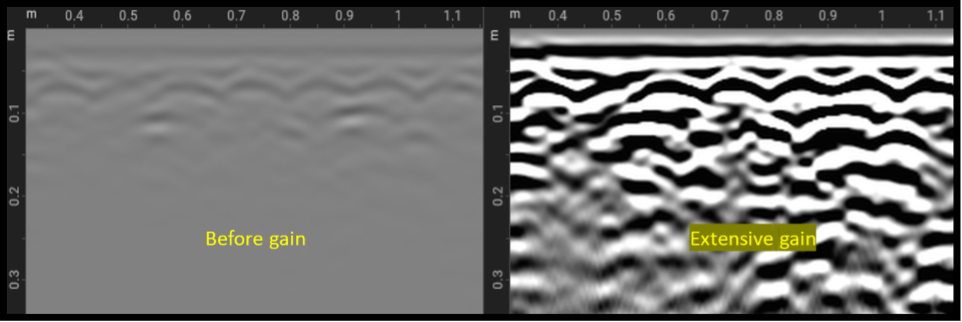
When applying gain, you need to be careful not to over-amplify the noise. When you apply too much gain, it amplifies not only the weak reflections but also the noise, which might mask meaningful reflections. In addition, since gain alters the amplitudes and also the relative amplitudes of the reflections, this means that you may lose the ability to distinguish between strong and weak reflectors based on their signal strength. Thus, extensive gain adjustments need to be avoided. Furthermore, if gain adjustment focuses too heavily on deep features, earlier reflections might become suppressed, leading to missed features. An example of applying extensive gain is shown below, where the signals have been saturated.

If multiple datasets are collected across different sections of the same survey and different gain settings are applied to each dataset, the data can be inconsistent making it harder to interpret. Thus, ensure consistent gain settings.

Best practices for gain adjustment: Begin by applying a lower gain to see how it affects the data and incrementally increase it as needed. Always evaluate the B-scans before and after gain to make sure the processed data still represent the subsurface accurately. Since signal attenuation varies with depth, a time-dependent gain is often more effective than constant.

Frequency filtering

Frequency filtering is the most common signal (applied to all signals, not only GPR signals) processing technique. A high-pass filter is utilized to attenuate low-frequency components and keeping the frequencies above that threshold. A low-pass filter is implemented to remove the high-frequency noise that may be present in the data (frequencies above a threshold) and keeps the frequencies below the threshold. Applying both results in a band-pass filter, where only a certain range of the frequencies contained in a signal is kept.

Real data always contain a certain form of noise, that in some cases can be extensive and therefore, frequency filtering is needed to remove it. Filtering can be implemented either in the time domain, such as a moving average smoothing filter, or more commonly in the frequency domain by a Fourier transform. An example of filtering frequencies is shown below, where on the right some of the noise in the data has been suppressed.

Note that extensive frequency filtering can suppress frequencies that are contained in meaningful reflections, and thus lead to data misinterpretation.

Migration

In a typical GPR B-scan image, which is collected with the antenna moving along a survey direction, a target appears as a hyperbola due to the different two-way propagation times of the EM wave for each antenna position. While processing the GPR data, it is common to correct this by transforming the unfocused B-scan image to a focused one. Migration is an advanced imaging technique used to transform the GPR image to a form more representative of the subsurface structure and more easily interpretable to the human eye. Assuming the EM wave velocity in the medium is known, migration collapses the hyperbolic responses of targets and places them to their correct spatial location. The final reconstructed image of the targets will resemble their true geometrical characteristics.

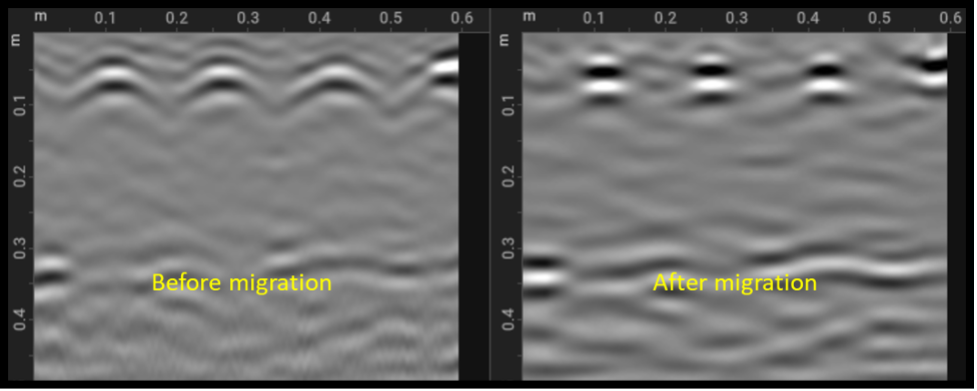
For the migration to work properly, a good estimate of the EM wave velocity is required. An example of performing migration with a correct velocity is shown below, where on the left is the B-scan before migration and on the right after, where the hyperbolas have collapsed.

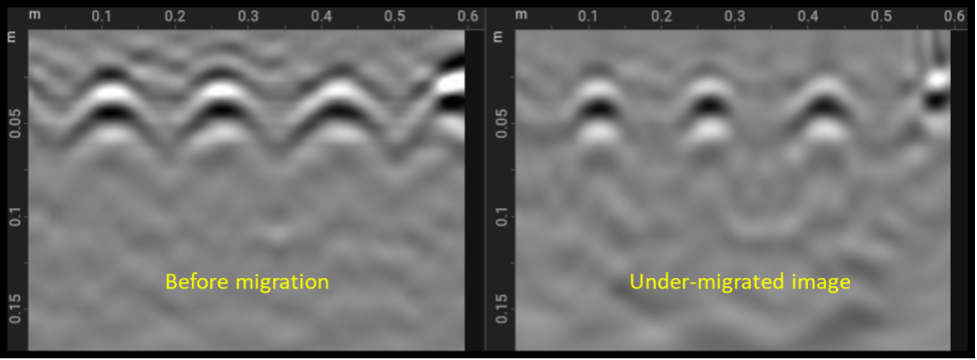
If the velocity set is too small, then the hyperbolas will not fully collapse, and we would have what is called under-migration. An example of under-migration is shown below, where it is visible that the hyperbolas have not fully collapsed as a result of selecting a velocity much smaller than the actual one.

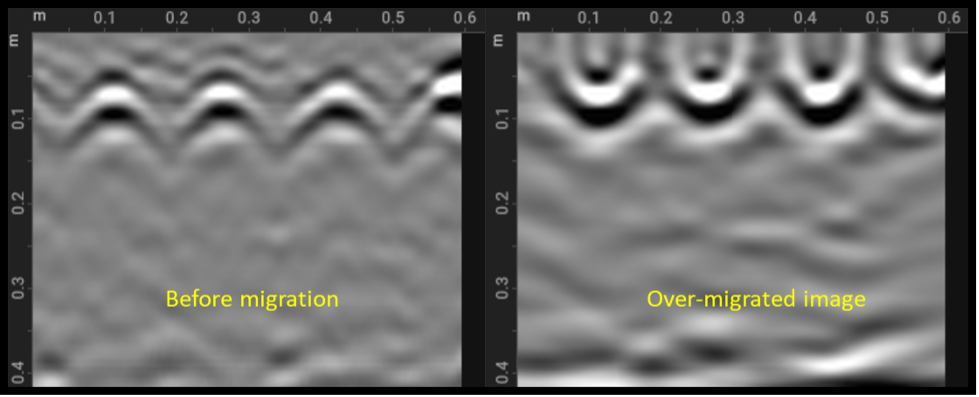
On the other hand, if the velocity is quite high, the hyperbolas will be essentially inverted and form the characteristic ‘smile’ patterns (over-migration). An example of an over-migrated image is shown below, with the characteristic ‘smiles’ being clearly visible. This is clearly not physical, but just an artifact created by processing due to high velocity.

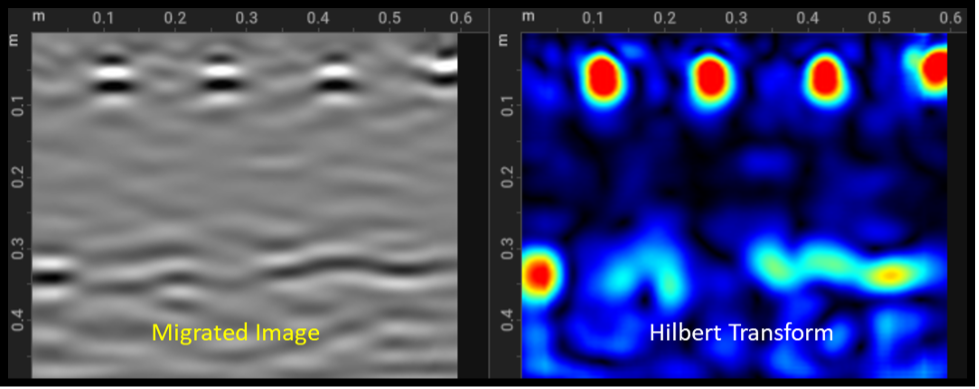
Hilbert transform

After migration, a commonly applied processing step is Hilbert transform. With Hilbert transform, the envelope of a signal is found, where a wavelet containing both positive and negative parts is converted to a wavelet with only positive components. This removes the oscillations of the signals and makes the interpretation of the data easier. An example is shown in the image below, where the Hilbert transform of the migrated image is plotted on the right.